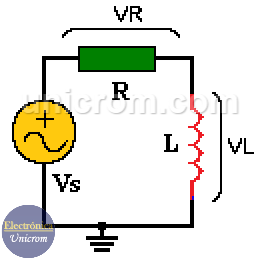
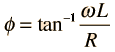Circuito RL serie en corriente alterna

En un circuito RL serie en corriente alterna, se tiene una resistencia y una bobina en serie. La corriente en ambos elementos es la misma.

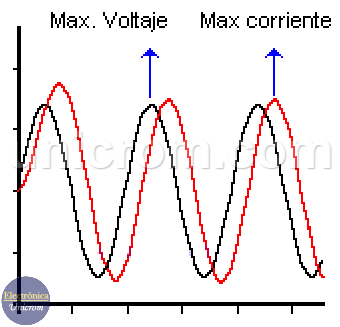
La tensión en la bobina está en fase con la corriente (corriente alterna) que pasa por ella (tienen sus valores máximos simultáneamente).

Pero el voltaje en la bobina está adelantado a la corriente que pasa por ella en 90º (la tensión tiene su valor máximo antes que la corriente). El valor de la fuente de voltaje que alimenta este circuito está dado por las siguientes fórmulas:

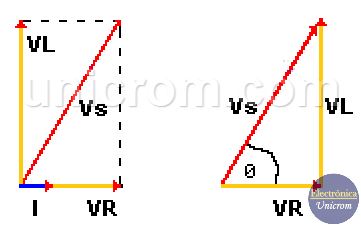
– Voltaje (magnitud) VS = (VR² + VL²)^1/2
– Angulo = /Θ = Arctang (Vl/VR).

Estos valores se expresan en forma de magnitud y ángulo. Ver el diagrama fasorial de tensiones.

Ejemplo: 47 /30° que significa que tiene magnitud de 47 y ángulo de 30 grados

La impedancia Z sería la suma (suma fasorial) de la resistencia y la reactancia inductiva. Y se puede calcular con ayuda de la siguiente fórmula:

• Para obtener la magnitud de Z se dividen los valores de Vs e I
• Para obtener el /Θ de Z se resta el ángulo de la corriente, del ángulo del voltaje.

Si la fuente de voltaje es: Vm senωt, la corriente es I = Im sen(ωt – ϕ).

Cálculo de impedancia y ángulo de fase en circuito RL serie

El valor de impedancia también se puede obtener con siguiente fórmula:

donde:

• L = Inductancia en Henrios
• R = valor de la resistencia en Ohmios
• ω = frecuencia angular en Radianes
• ω = 2πf
• π = 3.1416
• f = frecuencia en Hertz

El valor del ángulo de fase entre la corriente y el voltaje ϕ se puede obtener con la siguiente fórmula:

Ejemplo de cálculo de la impedancia y ángulo de fase

– Calcular la impedancia que tiene un circuito RL serie con los siguientes valores:

• R = 10000 ohmios,
• L = 100mH = 100 x 10^-3 henrios,
• Frecuencia de la fuente f = 800 Hertz

Usando las fórmulas anteriores:

Frecuencia angular es: ω = 2πf = (2)(3.1416)(800) = 5026.5 radianes
Impedancia es: Z = ( (10000)² + (5026.5)²(100×10^-3)² )^1/2 = 1 x 10⁴ ohmios

Cálculo del angulo de fase

Si la fuente de voltaje es: Vm senωt, la corriente es I = Im sen(ωt – ϕ).

ϕ = tan^-1( (5056.5)(100 x 10^-3) / 10000 ) = 2.88 grados.

Notas:

• Valores incluidos entre paréntesis elevado a la 1/2, equivale a una raíz cuadrada.
• Arctang( ) = tan^-1 ( )