En muchas ocasiones es necesario agrupar varias bobinas o inductores que están conectadas en serie o paralelo. Se presenta seguidamente el método para su simplificación y así encontrar su valor equivalente.
Bobinas o inductores en serie
El cálculo del inductor o bobina equivalente (LT) de bobinas en serie es similar al método de cálculo del equivalente de resistencias en serie, solo es necesario sumarlas.
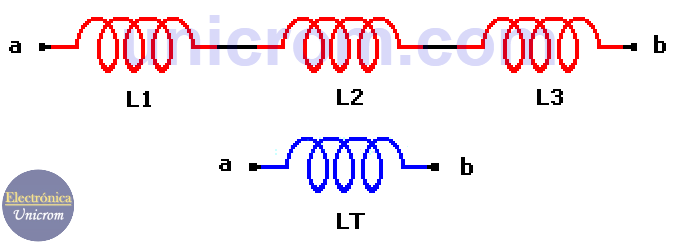
En el diagrama que sigue, hay 3 inductores o bobinas en serie. La fórmula a utilizar es: (sumatoria de los valores de los inductores): LT = L1 + L2 + L3.
Esto queda muy bien para este caso particular. Pero si se desea obtener el valor del inductor equivalente de más de 2 o 3 inductores, se usaría la siguiente fórmula:
LT = L1 + L2 + L3 +…+ LN, donde N es el número de bobinas colocadas en serie.
Bobinas o inductores en serie
Ejemplo 1. Se tienen 3 bobinas en serie con los siguientes valores:
- L1 = 10 mH
- L2 = 20 mH
- L3 = 30 mH
La bobina equivalente en serie es: LT = L1 + L2 + L3 = 10 mH + 20 mH + 30 mH = 60 mH
Bobinas o inductores en paralelo
El cálculo del inductor equivalente de varias bobinas en paralelo es similar al cálculo que se hace cuando se obtiene la resistencia equivalente de varias resistencias en paralelo.
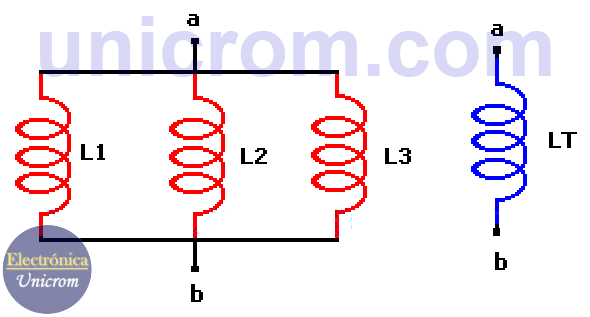
El caso que se presenta es para 3 inductores y se calcula con la siguiente fórmula: 1/LT = 1/L1 + 1/L2 + 1/L3
Bobinas o inductores en paralelo
Pero la fórmula se puede generalizar para cualquier número de inductores, con la siguiente fórmula:
1/LT = 1/L1 + 1/L2 + 1/L3 + … + 1/LN, donde N es el número de inductores que se conectan en paralelo.
Ejemplo 2: Se tienen 3 bobinas en paralelo con los siguientes valores:
- L1 = 20 mH
- L2 = 100 mH
- L3 = 50 mH
La bobina equivalente en paralelo es:
1/LT = 1/L1 + 1/L2 + 1/ L3 = 1/20 mH + 1/100 mH + 1/50 mH = 0.05 + 0.01 + 0.02 = 0.08. 1/LT = 0.08
sacando el inverso del resultado anterior, LT = 1/0.08 = 12.5 mH
Nota: bobina = inductor
Más tutoriales sobre bobinas / inductores
- Bobina – inductor
- Bobinas en serie y en paralelo
- La bobina y las corrientes – Factor de calidad
- Impedancia de una bobina – Reactancia inductiva
- Inductancia, Campo magnético, Fuerza contra electromotriz (FCEM)
- Cálculo de la inductancia de una bobina con núcleo de aire
- Circuito RL serie
- Respuesta al escalón unitario en un circuito RL
- Circuito RL paralelo en CA
- Bobina con núcleo metálico
Cuando se hace un calculo para obtener la capacitancia total de un arreglo en paralelo, los capacitores se suman. Se saca la inversa de las inversas cuando los capacitores están en serie, al contrario de lo que pasa con las resistencias.
Está mal una parte La asociación de bobinas en paralelo no se asemeja a la asociación de capacitores en paralelo; si a la asociación de resistencias en paralelo, escribiste mal amigo
en la página afirma que el equivalente de los inductores en “paralelo” es igual que al hallar la equivalente de los capacitores en paralelo. Al revisar el enlace y compararlo con la información dada, creo que hay que corregir el término “paralelo” pues es semejante a la equivalencia de capacitores en “serie” o de los “resistores” en paralelo.
gracias por su atención, esto es solo una critica constructiva 😉
Donde dice “… es similar al cálculo que se hace cuando se trabaja con condensadores en paralelo” debería decir: “resistencias en paralelo”
Tengo entendido que los condensadores en paralelo suman sus capacitancias, no la inversa de estas. Creo que está bien el cálculo de los inductores en paralelo, pero no es aplicable a condensadores en paralelo como dice.
Hola amigos
Muchas gracias por el aviso del error sobre las bobinas en paralelo.
El artículo ya fue corregido.
Saludos