Álgebra booleana – Álgebra de Boole
¿Para qué se usa el álgebra booleana? Cuando se trabaja con circuitos digitales, que son aquellos circuitos que se diseñan con compuertas AND, compuertas OR, compuertas NOT, etc., es muy común que al final de un diseño se tenga un circuito con un número de partes (circuitos integrados y otros) mayor al necesario.
Para lograr que el circuito tenga la cantidad de partes correcta (la menor posible) hay que optimizarlo (reducirlo).
Un diseño óptimo causará que:
- El circuito electrónico sea más simple.
- El número de componentes sea el menor.
- El precio de proyecto sea el más bajo.
- La demanda de potencia del circuito sea menor.
- El mantenimiento del circuito sea más fácil.
- Es espacio necesario (en el circuito impreso) para la implementación del circuito será menor.
En consecuencia que el diseño sea el más económico posible. Una herramienta para reducir las expresiones lógicas de circuitos digitales es la matemática de las expresiones lógicas, que fue presentada por George Boole en 1854, herramienta que desde entonces se conoce como álgebra de Boole.
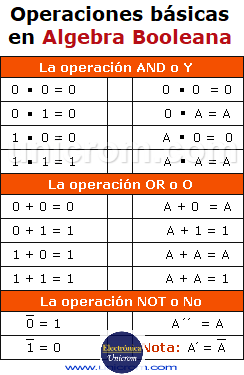
Las reglas del álgebra Booleana son:
Notas:
(punto): significa producto lógico.
+ (signo de suma): significa suma lógica.
Operaciones básicas en el álgebra booleana
Ley Distributiva, ley Asociativa, ley Conmutativa
Precedencia y Teorema de Morgan
Para asegurarse de que la reducción del circuito electrónico fue exitosa, se puede utilizar la tabla de verdad que debe dar el mismo resultado para el circuito simplificado y el original.