Convertidor voltaje a corriente constante con carga flotante
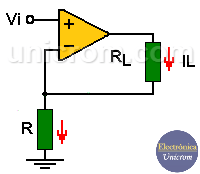
Esta configuración del convertidor voltaje a corriente constante está caracterizada básicamente en una entrada de voltaje (Vi), con una corriente de salida (IL).
Por lo que debido a la retroalimentación negativa tenemos un corto circuito virtual, por lo que Vi = VR y que IL = IR. Por lo tanto, IR = VR/R = Vi/R.
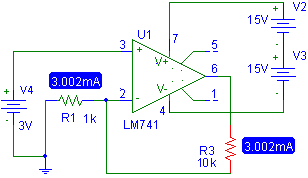
Observamos que la corriente de salida (en la carga) es función del voltaje de entrada, multiplicado por un factor (inverso de la resistencia) a esto se le llama factor de Transconductancia y por eso esta configuración también se le llama Amplificador de Transconductancia. Por ejemplo, si tenemos que IR = 3v/1k = 3mA
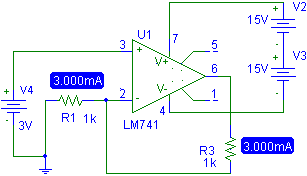
Fig. 1 Amplificador de Transconductancia. Con Vi = 3 y R1= 1k y R3 = 1k
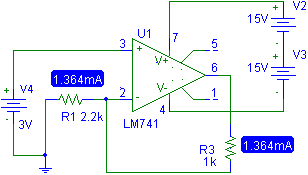
Ahora el mismo voltaje Vi pero con diferente resistencia R1. Ver Fig.2
Fig. 2 Amplificador de Transconductancia. Con Vi = 3 y R1= 2.2 K y R3 = 1 K
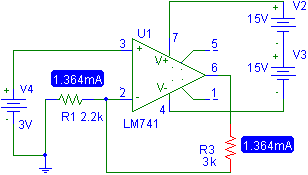
Ahora si a la resistencia R1 la dejamos igual pero cambiamos la resistencia R3:
Fig. 3 Amplificador de Transconductancia. Con Vi = 3V y R1= 2.2 K y R3 = 3K
Claro que la configuración tiene un límite. Tenemos que la resistencia de carga máxima: RLmax = (Vomax-Vi)/IL, RLmax = (Vcc-Vi)/IL, y sustituyendo IL también podemos expresar que: RLmax = (Vcc-Vi)*R/Vi, o que RLmax = (Vcc/Vi-1)*R
En este caso RL seria: RLmax = (Vcc/Vi-1)*R1 RLmax = (15/3 – 1)*1k RLmax = 4K
Entonces, con valores mayores a los 4K la Transconductancia ya no se cumplirá. Por lo que si agregamos una resistencia R3 = 10k, la corriente empezará a variar.
Fig. 4 Amplificador de Transconductancia. Con Vi = 3 y R1= 1K y R3 = 10K
La diferencia es muy pequeña pero conforme se aumente la resistencia R3, la corriente aumentará.
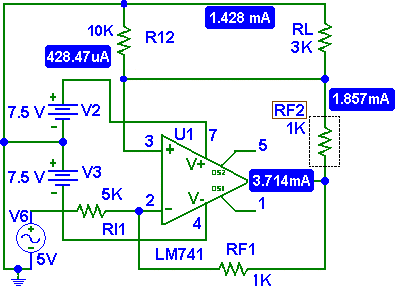
Convertidor voltaje a corriente constante con carga aterrizada
Considerando que la retroalimentación negativa es mayor que la positiva, el sistema es estable y se puede observar un corto circuito virtual en las entradas del OPAMP.
El análisis en esta configuración es muy parecida a la de carga flotante. La corriente que pasa por IRF1 = IRF2, por lo que (VI – VL) / RF1 = (VL – Vo)/RF2, factorizando Vo = VL – (-RF1/RI1)(VI – VL) IL = IF2 – II2 , IL = (Vo – VL)/RF2 – VL/R I2.
Si sustituimos Vo en la ecuación de IL tenemos: IL = – (RF1/RI1 x RF2) x Vi + ( RF1/RI1 x RF2 – 1 /RI2) x VL.
En esta última expresión IL depende de VL, por lo que debemos hacer cero ese término para así no depender de otros voltajes.
Por lo que si hacemos VL=0 (RF1/RI1 x RF2 – 1/RI2) x VL RF1/RI1 x RF2 = 1 /RI2
RF1/RI1 = RF2/RI2, entonces solo quedaría esta ecuación IL = – (RF1/RI1 x RF2) x Vi
pero como: RF1 = RF2 x RI1/RI2
IL = (-1/RI2) Vi.
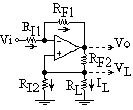
Un ejemplo sería: IL = -(1/5k) 5v, IL = 1mA, Ver Fig. 5
R2 = RL; RI2 = R7
Fig. 4 Amplificador de Transconductancia. Con Vi = 5 y RL= 1 y RI2 = 5K
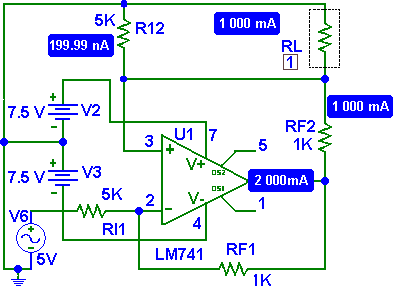
Vemos que la corriente es igual a 1mA con una resistencia de carga igual a un OHM, entonces si cambiamos la resistencia RL a 3K.
Fig. 5 Amplificador de Transconductancia. Con Vi = 5 y RL= 3K y RI2 = 5K
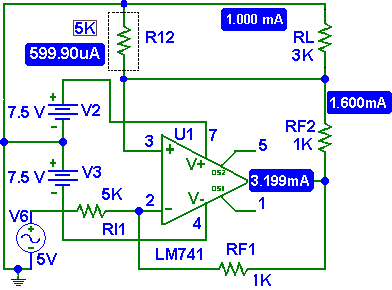
Ahora si cambiamos la resistencia RI2, obtendremos una variación en la corriente IL.
Fig. 5 Amplificador de Transconductancia. Con Vi = 5 y RL= 3K y RI2 = 10K
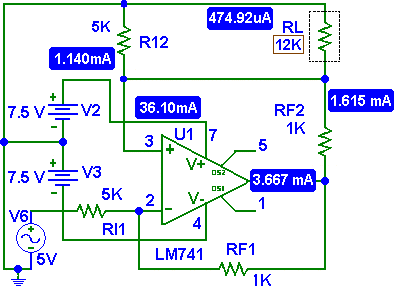
Volviendo al ejemplo de la FIg. 4 si cambiamos RL por un valor mayor a la RLmax y veremos que la corriente que por RL ya no será igual, esto quiere decir que el amplificador de transconductancia tiene una RLmax la cual no se debe de rebasar para así cumplir con esta configuración.
Fig. 6 Amplificador de Transconductancia. Con Vi = 5V y RL= 12K y RI2 = 10K
La manera de calcular esta RLmax es la siguiente:
RL = VL / IL (VI–VL)/RI = (VL–V0) / RF
VI x RF1 – VL x RF2 = VL x RI1 – V0 x RI1
VL = (VI x RF1 + V0 x RF1) / (RF1 + RI1)
IL = (- RF1 x VI) / (RI1 x RF2)
Si igualamos RL a toda la expresión quedará así:
Te puede interesar este convertidor de tensión a corriente con carga flotante y con carga aterrizada.
BIBLIOGRAFIA:
- http://www.imse.cnm.es/~huertas/SETI/Apendice1.pdf
- http://fisica.udea.edu.co/~gicm/lab_electronica/Propiedades20AO.pdf
Por: Jesús Ariel López V. (Draker) ariel_lopez@ieee.org, pabelo_el_yaqui@hotmail.com, México