¿Qué dice el teorema de superposición?
El teorema de superposición establece que, el efecto dos o más fuentes de voltaje y/o corriente tienen sobre un punto cualquiera en un circuito lineal, es igual a la suma de cada uno de los efectos de cada fuente tomados por separado, sustituyendo todas las fuentes de voltaje restantes por un corto circuito y las fuentes de corriente por circuitos abiertos.
El teorema de superposición ayuda a encontrar:
- Valores de tensión, en una posición de un circuito, que tiene más de una fuente de tensión y/o corriente.
- Valores de corriente, en un circuito con más de una fuente de tensión y/o voltaje.
Ejemplo de aplicación del Teorema de Superposición
Se desea saber cual es la corriente que circula por la resistencia RL (resistencia de carga) en un circuito con dos fuentes de voltaje.
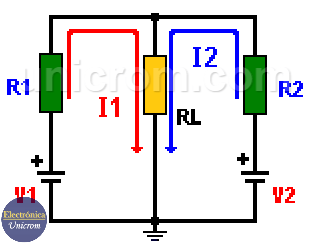
Teorema de Superposición – Circuito original
Los valores de las resistencias del circuito son las siguientes:
- R1 = 2 kiloohmios
- R2 = 1 kiloohmio
- RL = 1 kiloohmio
- V1 = 10 voltios
- V2 = 20 voltios
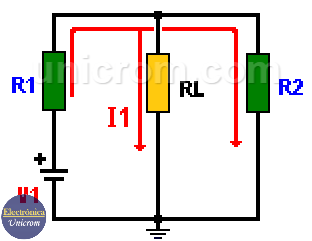
Como hay dos fuentes de voltaje, se utiliza una a la vez mientras se cortocircuita la otra. En el siguiente diagrama se toma en cuenta solo la fuente V1.
Teorema de Superposición – Primera fuente (V1)
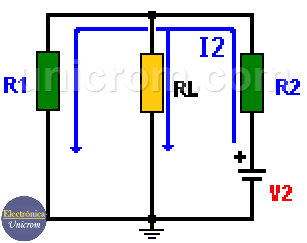
En el diagrama inferior se toma en cuenta solo la fuente V2.
De cada caso se obtiene la corriente que circula por la resistencia RL y después estos dos resultados se suman para obtener la corriente total en la resistencia RL.
Teorema de Superposición – Segunda fuente (V2)
Procedimiento y Cálculos
Primero se analiza el caso en que solo está conectada la fuente V1. Se obtiene la corriente total que entrega esta fuente obteniendo la resistencia equivalente de las dos resistencias en paralelo R1 y RL.
Req.= RL // R2 = 0.5 kiloohmios.
Nota: // significa paralelo.
A este resultado se le suma la resistencia R1 (R1 está en serie con Req.) y la resistencia total RT = R1 + Req. = 0.5 + 2 = 2.5 kiloohmios.
De esta manera se habrá obtenido la resistencia total equivalente en serie con la fuente V1.
Para obtener la corriente total se utiliza la Ley de Ohm:
I = V/R. I total = 10 Voltios / 2.5 kiloohmios = 4 mA (miliamperios.
Por el teorema de división de corriente se obtiene la corriente que circula por RL:
IRL = [I x RL // R2] / RL, donde RL // R2 significa el paralelo de RL y R2 (se obtuvo antes Req. = 0.5 kiloohmios).
Reemplazando: IRL = [4 mA x 0.5 kiloohmios] / 1 kiloohmio = 2 mA. (miliamperios).
El caso de la fuente V2 se desarrolla de la misma manera, solo que se deberá cortocircuitar la fuente V1. En este caso la corriente se debe solo a la presencia de V2 y es 8 mA. (miliamperios). La corriente tiene el mismo sentido que la corriente encontrada debido a la fuente V1 y por eso se suman.
Sumando las dos corrientes se encontrará la corriente que circula por la resistencia RL del circuito original. Corriente total = IT = 2 mA. + 8 mA. = 10 mA. (miliamperios).
Nota: Si las corrientes tuvieran sentidos opuestos se deben restar y el valor de la corriente resultante tendrá el sentido de la corriente de mayor valor.
Si se tiene la corriente total en la resistencia RL, también se puede obtener su voltaje en esta resistencia con solo utilizar la ley de Ohm: VL= IT x RL.