¿Por qué se usa el sistema de numeración Hexadecimal?
El sistema de numeración hexadecimal (base 16) se utiliza principalmente para la simplificación de la representación de números binarios y para el manejo digital de los colores.
El sistema hexadecimal, a diferencia del sistema decimal, necesita 16 cifras y/o letras para poder expresar una cantidad. Ver la siguiente lista: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F (si se cuentan las letras y números anteriores se tienen 16.)
El sistema hexadecimal y el sistema binario
Una relación útil entre el sistema hexadecimal y el decimal no es evidente, sin embargo si lo es con el sistema binario.
El número 255 en decimal se expresa en binario como 8 “unos” (11111111). Este y otros números en binario son confusos de interpretar, pero si lo transformamos en sistema hexadecimal, tendrá solo dos cifras en vez de 8. De lo anterior se deduce que: expresar, recordar y utilizar este formato es más fácil.
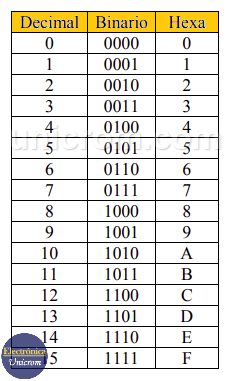
En la siguiente tabla se ve una comparación de los números el Sistema decimal, binario y hexadecimal.
Tabla de conversión de los Sistemas Decimal, Binario y Hexadecimal
Ejemplos de pasar del sistema binario al hexadecimal:
- 111111112 = FF16
- 101010102 = AA16
- 00111100 = 3C16
Como se puede ver es más legible el sistema hexadecimal. Primero se convierten las primeras 4 cifras del número binario y después los siguientes.
Para convertir los números entre estos dos sistemas, basta con leerlos de la tabla anterior.
El sistema de numeración hexadecimal y el sistema decimal
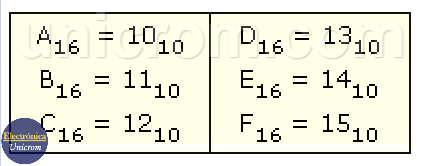
Se puede ver que en el Sistema de Numeración Hexadecimal se utilizan las letras de la “A” a la “F” para obtener los números del 10 al 15 en base 10.
Para pasar un número decimal a hexadecimal
Se divide el número en decimal por 16, hasta que el cociente de cero y después se leen los números que quedan da abajo hacia arriba.
Ejemplo 1: Si tengo el número 274110 y lo deseo pasar a hexadecimal, hago lo siguiente:
Paso 1
- 2741 / 16 = 171, quedan 5
- 171 / 16 = 10, quedan 11
- 10 / 16 = 0, quedan 10
Paso 2
Se leen los números que “quedan” de abajo hacia arriba: 10, 11, 5. Consultando la tabla anterior se obtiene que el número en hexadecimal es: AB516.
Ejemplo 2: Si tengo el número 4732110 y lo deseo pasar a hexadecimal, hago lo siguiente:
Paso 1
- 47321 / 16 = 2957, quedan 9
- 2957 / 16 = 184, quedan 13
- 184 / 16 = 11, quedan 8
- 11 / 16 = 0, quedan 11
Paso 2
Se leen los números que “quedan” de abajo hacia arriba: 11, 8, 13, 9. Consultando la tabla anterior se obtiene que el número en hexadecimal es: B8D916.
Para pasar un número en hexadecimal a decimal:
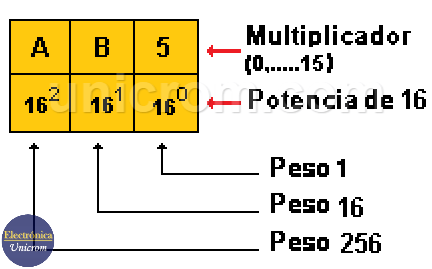
Un número en el sistema hexadecimal se divide en cifras con diferente peso: 1, 16, 256, 4096, 65536,…. etc y se coloca como en el siguiente ejemplo. En este caso tenemos el número AB516 y se colocan los “pesos” correspondientes debajo de cada cifra. Ver el siguiente diagrama.
Al final se suman los valores en decimal correspondientes a cada cifra en hexadecimal, como se ve en gráfico inferior. Ver los valores de los “pesos” correspondientes (1, 16, 256, … etc) a la posición de cada cifra en el número hexadecimal.