El Sistema de Numeración Binario (base 2)
El Sistema de Numeración Binario, a diferencia del Sistema de Numeración Decimal, donde son permitidos 10 cifras (del 0 al 9), solo necesita dos (2) cifras: el “0” y el “1”.
El Sistema de Numeración Binario es de especial importancia en la electrónica digital, donde solo son posibles dos valores: el “1” o valor de voltaje “alto” y el “0” o nivel de voltaje “bajo”. Los valores de “1” y “0” se asocian con:
“nivel alto” y “nivel bajo”, “cerrado” y “abierto”, “encendido” y “apagado”, “conectado” y “desconectado”, “high” y “low”, “on” y “off”, etc. Ver Introducción a los sistemas digitales.
Para evitar confundirse con los otros sistemas de numeración se acostumbra colocar al final del número binario un “2” como subíndice. Ejemplos: 10112, 1112, 1010012.
¿Cómo pasar de Binario a Decimal?
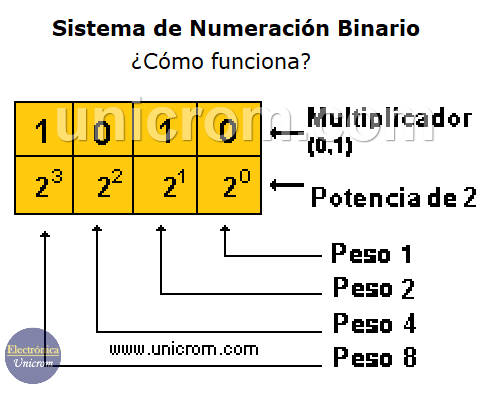
Analizar el siguiente gráfico. Un número en el Sistema de Numeración Binario se divide en cifras con diferente peso: 1, 2, 4, 8, 16, 32, 64, 128, . . . . , etc. Cada peso tiene asociado una potencia.
En el primer número (de derecha a izquierda) la potencia de dos es 20, en el segundo número la potencia de dos es 21 y así hasta el último número del lado izquierdo.
Entonces para formar el número 10102: (el número 10 en binario) se hace lo que se muestra en la siguiente imagen.
¿Cómo pasar de Decimal a Binario?
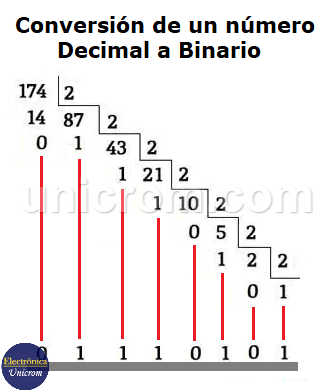
Para pasar un número decimal a binario, se hacen divisiones sucesivas del número en decimal por 2, como se ve en la siguiente imagen.
Estas sucesivas divisiones dan como residuos “0” o “1”. Estos “0” y “1” más el cociente de la última división forman el número en binario que se lee de derecha a izquierda.
Entonces, el número 17410 (decimal) es igual a 101011102 (binario).
La parte decimal en el Sistema de numeración Binario
En los números binarios también se toman en cuenta los decimales. Por ejemplo: 11100,1012
En el caso de los números con parte decimal se establece que el peso que tienen las cifras de la parte decimal de la siguiente manera:
- Primera cifra después de la coma tiene un peso de 1/2
- Segunda cifra después de la coma tiene un peso de 1/4
- Tercera cifra después de la coma tiene un peso de 1/8
- Cuarta cifra después de la coma tiene un peso de 1/16
- etc.
Ejemplo: Convertir el número anterior: 11100,10102, a su equivalente en decimal utilizando el peso que tiene cada cifra.
- 1 – 1 x 16 = 16
- 1 – 1 x 8 = 8
- 1 – 1 x 4 = 4
- 0 – 0 x 2 = 0
- 0 – 0 x 1 = 0
coma (,)
- 1 – 1 x 1/2 = 0,5
- 0 – 0 x 1/4 = 0
- 1 – 1 x 1/8 = 0,125
- 0 – 1 x 1/16 = 0
Sumando todos los resultados anteriores se obtiene el valor equivalente en el sistema de numeración decimal.
16 + 8 + 4+ 0 + 0 + 0.5 + 0 + 0.125 = 28.625 en el sistema de numeración decimal (28.62510)



Gracias me fue de ayuda!