Resistencias en paralelo – Resistores en paralelo

Resistencias en paralelo – Resistores en paralelo

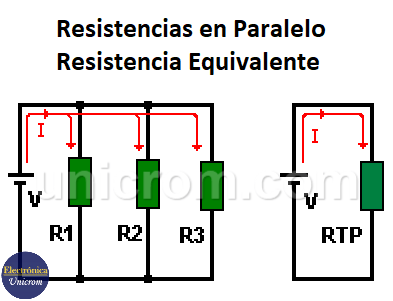
En el circuito de resistores en serie, la corriente eléctrica circula solo por un camino. En el circuito de resistencias en paralelo, la corriente se divide y circula por varios caminos (cada una de las resistencias). En este caso se tienen 3 resistencias y parte de la corriente total circula por cada una de ellas.

Estas resistencias están unidas por sus dos extremos como se muestra en la figura.

La corriente (I) que suministra la fuente de voltaje V es la misma en el circuito original (con R1, R2 y R3) y en el equivalente. (ver la figura)

En el circuito original, la corriente se divide y pasa por cada una de las resistencias, pero el total de la suma de las corrientes de cada resistencia es siempre igual a la corriente que suministra la fuente de voltaje.

Resistencia equivalente de resistencias en paralelo

La resistencia equivalente de un circuito de resistencias en paralelo es igual al recíproco de la suma de los inversos de las resistencias individuales, así, la fórmula para un caso de 3 resistencias es:

La fórmula para dos resistencias en paralelo muy usada es: Rtp = (R1 x R2)/ (R1+R2)

En nuestro caso, como tenemos 3 resistencias utilizaremos la siguiente fórmula general

Rtp (resistencia total en paralelo) = 1 / ( 1/R1 + 1/R2 + 1/R3 )

Para el caso general con “n” resistencias en paralelo, la fórmula es:

Rtp = 1 / (1/R1 + 1/R2 + 1/R3 + …….. + 1/Rn)

La conductancia equivalente de resistencias en paralelo

Presentando esta fórmula anterior de manera ligeramente diferente:

1/Rtp = 1/R1 + 1/R2 + 1/R3   y… utilizando la fórmula de la conductancia (G = 1/R) se tiene que:

• Conductancia equivalente es igual a la suma de las conductancias: Gtp = G1 + G2 + G3  o
• Conductancia equivalente es igual a la suma de los inversos de las resistencias: Gtp = 1/R1 + 1/R2 + 1/R3

La fórmula general de la conductancia para “n” resistencia en paralelo es:

• Gtp = G1 + G2 + G3 + ……. Gn
• Gtp = 1/R1 + 1/R2 + 1/R3 + ….. 1/Rn

donde “n” es el número de resistencias

Como se sabe que la conductancia total es el inverso de la resistencia total Gtp = 1/Rtp, despejando Rtp la resistencia equivalente de resistencias en paralelo es: Rtp = 1/Gtp.

La unidad de la conductancia es el Siemens. Ver definición de unidades comunes.

Ejemplos de cálculo de resistencias en paralelo

Ejemplo 1

Obtener la resistencia equivalente de 2 resistencias en paralelo R1= 100 ohmios y R2 = 300 ohmios.

• 1/Rtp = 1/R1 + 1/R2
• 1/Rtp = 1/100 + 1/300 = 0.01 + 0.0033 = 0.0133
• 1/Rtp = 0.0133 …, despejando Rtp
• Rtp = 1/0.0133 = 75 ohmios

• Gtp = G1 + G2
• G1 = 1/100 = 0.01 siemens
• G2 = 1/300 = 0.0033 siemens
• Gtp = G1 + G2 = 0.0133 siemens

Comprobando con Gtp = 1/Rtp,   0.0133 = 1/75. Entonces Rtp = 75 ohmios

Ejemplo 2

Obtener la resistencia equivalente de 3 resistencias en paralelo R1 = 1 K, R2 = 470 ohmios y R3 = 2.2 K.

1 K = 1000 ohmios, 2.2 K = 2200 ohmios

• 1/Rtp = 1/R1 + 1/R2+ 1/R3
• 1/Rtp = 1/1000 + 1/470 + 1/2200 = 0.001 + 0.0021 + 0.0005 = 0.0036
• 1/Rtp = 0.0036…. despejando Rtp
• Rtp = 1/0.0036 = 277.78 ohmios

La conductancia equivalente es: 

• Gtp = G1 + G2 + G3
• G1 = 1/1000 = 0.001 siemens
• G2 = 1/300 = 0.0021 siemens
• G3 = 1/2200 = 0.0005 siemens
• Gtp = G1 + G2 + G3 = 0.0036 siemens

Comprobando con Gtp = 1/Rtp,   0.0036 = 1/277.78. Entonces Rtp = 277.78 ohmios

El método funciona igual para “n” resistencias en paralelo.

Casos especiales con las resistencias en paralelo

• Cuando las resistencias es paralelo son iguales (R), la resistencia equivalente Rtp = R/n, donde “n” es igual al número de resistencias en paralelo.

Ejemplo: 3 resistencias de 330 ohmios se conectan en paralelo. El valor de la resistencia equivalente es:

Rtp = 330 ohmios/3 = 110 ohmios

• Cuando los valores de las resistencias son muy diferentes, el valor de la resistencia equivalente está más cercano al valor de la resistencia más pequeña.

Ejemplo: 2 resistencias, R1 = 1000 ohmios y R2 = 10 ohmios. Usando la fórmula Rtp = (R1 x R2)/ (R1+R2),

Rtp = (1000 x 10)/(1000 + 10) = 10000/1010 = 9.9 ohmios