Para hacer el análisis y la simplificación de circuitos mixtos solo es necesario trabajar ordenadamente y conocer las fórmulas de simplificación de resistencias en serie y resistencias en paralelo.
¿Qué son circuitos mixtos? Circuitos mixtos son aquellos que se conforman por combinaciones de circuitos en serie y circuitos en paralelo.
Simplificar un circuito serie de resistencias en serie o un circuito de resistencias en paralelo en forma individual es muy sencillo, la situación es diferente cuando se tiene que hacer una simplificación de circuitos mixtos que está compuesto por combinaciones de resistencias en serie y paralelo.
Proceso a seguir para simplificar circuitos mixtos
Para simplificar un circuito mixto y obtener la resistencia equivalente, se sigue el siguiente procedimiento:
– Se reordena o re acomoda el circuito que se desea simplificar, de modo que vean claramente las partes dentro del circuito, que ya estén conectados en serie y paralelo.
– A cada una de estas partes se le asigna un nuevo nombre, por ejemplo RA, RB, RC, RD, etc.
– Se obtiene la resistencia equivalente de cada parte con ayuda de las fórmulas ya conocidas. (resistencias en serie y resistencias en paralelo).
– Se reemplazan las partes dentro del circuito original con los valores de las resistencias equivalentes (RA, RB, etc.) obtenidas en el paso anterior. Se analiza el circuito resultante y se busca combinaciones (partes) adicionales, serie y paralelo que hayan sido creadas.
– Se repite nuevamente el proceso a partir del paso 2, con nombres diferentes para las resistencias equivalentes para evitar la confusión (ejemplo: RX, RY, RZ, etc.), hasta obtener una sola resistencia equivalente final de todo el circuito.
Ejemplo de simplificación de un circuito mixto
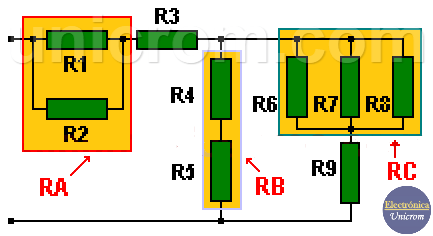
Observando el siguiente gráfico y utilizando los valores de resistencias a continuación:
- R1 = 120, R2 = 250, R3 = 68, R4 = 47, R5 = 68. (todas en ohmios)
- R6 = 5, R7 = 4, R8 = 2, R9 = 1.2. (todas en kiloohmios)
– RA = R1//R2 = R1 x R2 / (R1 + R2) = 120 x 250 / (120 + 250) = 81 ohmios
– RB = R4 + R5 = 47 + 68 = 115 ohmios
– RC = R6//R7//R8 = 1/(1/R6 + 1/R7 + 1/R8) = 1/( 1/5 K + 1/4 K + 1/2 K) = 1053 ohmios
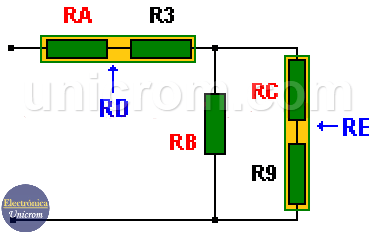
Reemplazando los valores equivalentes obtenidos en el circuito original se obtiene:
Este circuito se puede volver a simplificar obteniendo las resistencias equivalentes de la conexión serie de RA – R3 y RC – R9, entonces:
– RD = RA + R3 = 81 + 68 = 149 ohmios
– RE = RC + R9 = 1053 + 1200 = 2253 ohmios
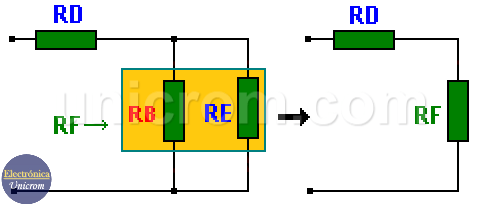
Y reemplazando estos últimos datos, se obtiene el siguiente circuito:
En este último circuito se puede ver que RB y RE están en paralelo y reduciendo se obtiene una nueva resistencia equivalente RF, que estará en serie con RD:
RF = RB//RE = RB x RE / (RB + RE) = 115 x 2253 / (115 + 2253) = 109 ohmios
RF estará en serie con RD con la que bastará hacer la suma de sus valores para obtener la resistencia final equivalente. Entonces: R equivalente final = Req = RF + RD = 109 + 149 = 258 ohmios.