Respuesta transitoria de un circuito RL serie

Respuesta transitoria de un circuito RL serie

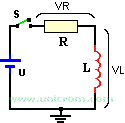
Para analizar la respuesta transitoria de un circuito RL serie, se colocan una bobina / inductor y una resistencia conectados como se muestra en la siguiente figura. Se incluye también una batería y un interruptor. Todos en serie.

Cuando se cierra el interruptor S, los elementos R y L son recorridos por la misma corriente. Esta corriente, que es variable (se llama transitoria hasta llegar a su estado estable), crea un campo magnético. Este campo magnético genera una corriente cuyo sentido está definido por la Ley de Lenz. La ley de Lenz establece que:

“La corriente inducida por un campo magnético en un conductor tendrá un sentido que se opone a la corriente que originó el campo magnético.”

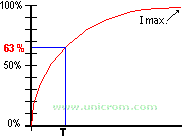
Es debido a esta oposición, que la corriente no sigue inmediatamente a su valor máximo, sino que se comporta de la siguiente forma:

La duración de la carga está definida por la constante de tiempo T. La bobina alcanza su máxima corriente cuando t (tiempo) = 5 x T. En otras palabras, cuando han pasado el equivalente a 5 constantes de tiempo. Donde T = L/R

La ecuación de la línea de carga anterior tiene la siguiente fórmula: – IL(t) = IF x ( 1 – e ^-t/T) Donde:

• IL(t) = corriente instantánea en la bobina o inductor
• IF = corriente máxima
• e = base de logaritmos naturales (aproximadamente = 2.73)
• t = tiempo
• T = constante de tiempo = L/R
• L y R son los valores de la inductancia y la resistencia respectivamente

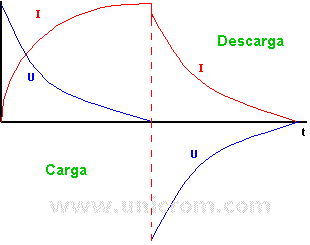
Las forma de onda de la tensión y la corriente en el proceso de carga y descarga en un inductor se muestran en las siguientes figuras:

• I_L(t) (descarga) = Io x e^-t/T
• V_L(t) (carga) = Vo x e^-t/T
• V_L(t) (descarga) = Vo x e^-t/T

Donde:

• Io = corriente inicial de descarga
• Vo = tensión inicial de carga o descarga
• IL(t) = corriente instantánea en la bobina
• VL(t) = tensión instantánea en la bobina
• e = base de logaritmos naturales (aproximadamente = 2.73)
• t = tiempo
• T = constante de tiempo = L/R
• L y R son los valores de la inductancia y la resistencia respectivamente

Nota: inductor = bobina, resistencia = resistor