¿Cómo calcular un Transformador con Datos del Núcleo?

Potencia de un núcleo de transformador

El primer dato que hay que conocer para calcular un transformador son los vatios que es capaz de suministrar el núcleo que tenemos. Este dato, como ahora veremos, se obtiene midiendo la sección central del núcleo.

En la práctica hay que medir la longitud L y la altura H del paquete de láminas (ver fig.3- 4), luego se multiplicará L x H para obtener el valor de su sección en milímetros cuadrados.

Considerando que todas las láminas tienen dispersiones de las líneas de fuerza y que, al insertarlas en el cartucho, nunca lograremos apretarlas como lo hace una máquina empaquetadora, habrá siempre un microscópico espacio entre una y otra que reducirá la sección neta.

La sección bruta de un paquete de láminas tendremos que multiplicarla siempre por 0,95 para obtener la sección neta = Sn. Suponiendo que el núcleo que tenemos tenga una L de 22 mm y una H de 38 mm, tendremos una sección bruta de: 22 x 38 = 836 mm² y una sección neta de: 836 x 0,95 = 794 mm²

Sabiendo la sección neta, que llamaremos Sn, para obtener la potencia en vatios de este núcleo podemos esta fórmula:  vatios = (Sn x Sn): 14.000

Potencia teórica y Potencia real de núcleo

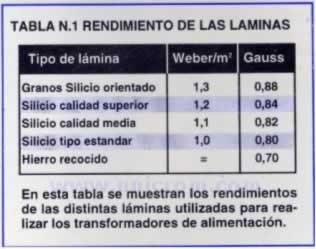
Luego este núcleo debe ser capaz, teóricamente, de suministrar una potencia de: (794 x 794): 14.000 = 45 vatios teóricos. Hemos precisado vatios teóricos porque, según el tipo de lámina empleada, variará su rendimiento (ver Tabla N.1) y consecuentemente también su potencia real:

• 45 x 0,88 = 39,6 vatios reales
• 45 x 0,84 = 38,8 vatios reales
• 45 x 0,82 = 36,9 vatios reales
• 45 x 0,80 = 36,0 vatios reales
• 45 x 0,70 = 31,5 vatios reales

Por este motivo, en el mercado podemos encontrar transformadores muy pequeños capaces de suministrar la misma potencia que un transformador de dimensiones notablemente mayores.

Como en la mayor parte de los casos no se sabe el tipo de lámina que se obtiene de un viejo transformador, conviene, curándonos en salud, elegir un rendimiento del 0,82. Por tanto, la fórmula indicada anteriormente se modificará del siguiente: vatios = [(Sn x Sn): 14.000] x 0,82

Si el rendimiento de nuestra lámina fuera mayor, por ejemplo de 0,84 o de 0,88 mejor, porque obtendremos un transformador que no se calentará aunque trabaje muchas horas. Las láminas de hierro recocido, con un rendimiento del 0,70, no se utilizan hoy, por tanto, es inútil tomarlas en consideración.