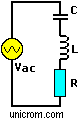Circuito RLC serie – Angulo de fase

Angulo de fase en un circuito RLC serie

Analizando un circuito RLC en serie, la corriente (corriente alterna) que pasa por la resistencia, el condensador y la bobina es la misma y la tensión Vac es igual a la suma fasorial de la tensión en la resistencia (V_R) y la tensión en el condensador (V_C) y la tensión en la bobina V_L. Vac = V_R+V_C+V_L (suma fasorial)

La impedancia total del circuito RLC anterior es: Z_T = R + X_L + X_C (suma vectorial) ó R + j(X_L – X_C) ó R + jX , donde:

• X_C = reactancia capacitiva
• X_L = reactancia inductiva
• R = valor del resistor
• X = la diferencia de X_L y X_C. (Si X es positivo predomina el efecto inductivo. Si X es negativo predomina el efecto capacitivo.

La corriente en el circuito se obtiene con la Ley de Ohm:

I = V/Z = Vac/Z_T = Vac/( R + jX)^1/2  y  El ángulo de fase es: 0 = arctan (X/R)

Nota: El paréntesis elevado a la 1/2 significa raíz cuadrada.

Ángulos de fase en un circuito RLC

Analizando los tutoriales circuitos RC en serie y circuitos, RL en serie, se puede iniciar el análisis de los ángulos de fase de un circuito RLC. El proceso de análisis se puede realizar en el siguiente orden:

1. Al ser un circuito en serie, la corriente I es la misma por todos los componentes, por lo que la tomamos como vector de referencia
2. V_R (voltaje en la resistencia) está en fase con la corriente, pues la resistencia no causa desfase.
3. V_L (voltaje en la bobina) adelanta a la corriente I en 90º
4. V_C (voltaje en el condensador) atrasada a la corriente I en 90º
5. Los vectores VL y VC se pueden sumar pues están alineados.
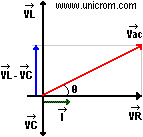
6. Vac (voltaje total) se obtiene de la suma vectorial de V_R y (V_L – V_C).

Angulos de fase de un circuito RLC serie

Nota: El signo menos delante de V_C en el punto 6 se debe a que esta tensión tiene dirección opuesta a V_L. En el diagrama se supone que V_L es mayor que V_C, pero podría ser lo contrario.

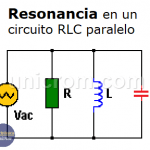
Un caso especial aparece cuando V_L y V_C son iguales. (V_L = V_C). En este caso V_R = Vac. La condición que hace que V_C y V_L sean iguales se llama condición de resonancia, y en este caso aún cuando en le circuito aparecen una capacidad y una inductancia, este se comporta como si fuera totalmente resistivo. Este caso aparece para una frecuencia especial, llamada frecuencia de resonancia. (f0)