¿Qué dice el Teorema de Millman?
El teorema de Millman establece que cuando hay varias fuentes de voltaje conectadas en paralelo, y cada una de ellas con su respectiva resistencia interna (Ri), el arreglo puede ser reemplazado por una sola fuente de voltaje (VM) en serie con una resistencia equivalente (RM).
¿Para qué se necesita el Teorema de Millman?
Hay muchos casos, en que se tiene de más de una fuente de voltaje para suministrar energía. Algunos ejemplos de este caso son:
- Un banco de baterías en paralelo para un sistema de alimentación de emergencia.
- Una serie de generadores de electricidad conectados en paralelo, etc.
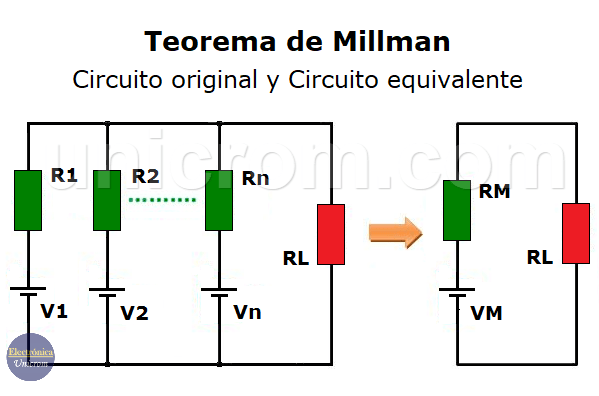
Cada una de estas fuentes de voltaje, que están en paralelo, tiene una resistencia interna diferente (resistencia propia de cada fuente) y todo el conjunto de fuentes alimentan una carga (RL). Ver diagrama del circuito original (lado izquierdo del diagrama).
El teorema de Millman nos muestra un método sencillo para obtener un circuito equivalente (lado derecho del diagrama).
Teorema de Millman – Circuito original y circuito equivalente
Procedimiento para encontrar el circuito equivalente
- Se obtiene “RM”, que es el valor de la resistencia equivalente en paralelo de todas las resistencias que van en serie con las fuentes de tensión.
1/RM = 1/REq = 1/R1 + 1/R2 + ….. + 1/Rn - Se obtiene “VM” con ayuda de la siguiente fórmula:
VM = (V1/R1 + V2/R2 + ….. + Vn/Rn) / (1/R1 + 1/R2 + 1/Rn).
Si fueran 3 o más fuentes con sus respectivas resistencias internas, el proceso sería el mismo. Al final se obtiene un circuito que consiste de una fuente de voltaje en serie con una resistencia, que se conecta a la carga. En nuestro caso: RL.
La fuente de voltaje tiene el valor VM y el resistor el valor RM. El diagrama que se muestra (lado derecho del diagrama) es el circuito equivalente de Millman.
Ejemplo:
Un circuito similar al anterior con 3 fuentes de voltaje, 3 resistencias en serie y una resistencia de carga.
- V1 = 96 V, R1 = 240 ohmios
- V2 = 40 V, R2 = 200 ohmios
- V3 = 80 V, R3 = 800 ohmios
- RL = 192 ohmios
Obteniendo el valor de RM
1/RM = 1/R1 + 1/R2 + 1/R3 = 1/240 + 1/200 + 1/800 = 0.01417
1/RM = 0.01417 entonces: RM = 96 ohmios.
Obteniendo el valor de VM
VM = (V1/R1 + V2/R2 + V3/R3) / (1/RM)
VM = 0.4 + 0.2 + 0.1) / (0.01417) = (0.7) (96) = 67.2 voltios. Entonces VM = 67.2 voltios.
Los valores de RM y VM encontrados se reemplazan en el circuito anterior (ver gráfico anterior a la derecha) para obtener el circuito equivalente de Millman para este ejemplo.



Excelente