Análisis de Mallas – Pasos a seguir – Ejemplo

El método de análisis de mallas

El método de análisis de mallas es muy utilizado para resolver circuitos resistivos (circuitos con solo resistencias) lineales (este método, un poco más ampliado, se aplica a también a circuitos resistivos – reactivos que incluyen condensadores y bobinas).

Utilizando este método se obtienen los valores de las corrientes en todas las resistencias que haya en el circuito. Conociendo estos valores se pueden obtener otros datos como: voltajes, potencias, etc., en todos los elementos del circuito. Este método se basa en la ley de tensiones de Kirchhoff:

La suma de las caídas de tensiones en todas las resistencias es igual a la suma de todas las fuentes de tensión en un camino cerrado en un circuito.

Pasos a seguir para el análisis por el método de mallas:

1. Graficar el circuito de manera que no exista ningún conductor (de ser posible) que cruce sobre otro.
2. Convertir las fuentes de corriente en fuentes de tensión
3. Dibujar las corrientes que circulan por el circuito con las puntas de las flechas indicando que van en el sentido de las agujas del reloj. Las corrientes se denominan I₁, I₂, I₃, …, etc. Ver ejemplo al final.
4. Formar una tabla con las ecuaciones obtenidas del circuito (con ayuda de la ley de voltajes de Kirchhoff). El número de filas de la tabla es el mismo que el número de corrientes establecidas en el paso 3.
5. Las columnas con las incógnitas se ponen al lado izquierdo del signo igual y la columna con los valores constantes al lado derecho del signo de igualdad.

También te puede interesar el Método de análisis de nodos

Ejemplo práctico del método de análisis de mallas

Para obtener los valores de las corrientes en el siguiente circuito se siguen los siguientes pasos.

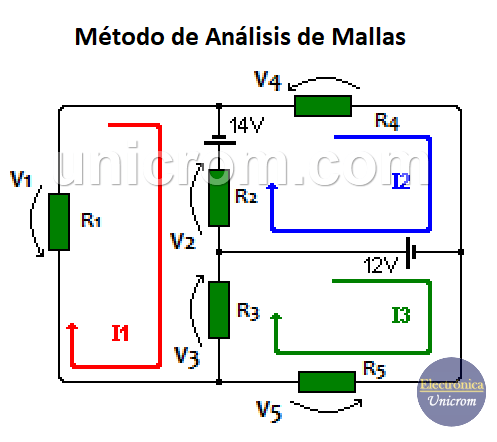
Ejemplo de análisis de mallas en un circuito resistivo

• Se establecen las mallas para la corriente I1 (roja), I2 (azul) e I3 (verde)
• Para la malla de la corriente I1, se suman los voltajes en sentido horario:  V1 + V2 + V3 – 14 V = 0  (1)
• Para la malla de la corriente I2: se suman los voltajes en sentido horario: -V2 + 14 V + V4 – 12 V = 0  (2)
• Para la malla de la corriente I3: se suman los voltajes en sentido horario: -V3 -12 V + V5 = 0  (3)

Nota: Cuando el voltaje y la corriente en una resistencia tienen el mismo sentido, el voltaje se toma como negativo. Ver el voltaje V2 en la malla de corriente I2 y el voltaje V3 en la malla de la corriente I3.

Reemplazando los valores de voltaje correspondientes (con la ley de Kirchhoff), se obtienen:

• V1 = I1 x R1
• V2 = (I1 – I2) x R2
• V3 = (I1 – I3) x R3
• V4 = I2 x R4
• V5 = I3 x R5

Reemplazando los valores de voltaje anteriores en las fórmulas (1), (2) y (3) se obtienen:

• Para la malla de la corriente I1:  I1 x R1  + (I1 – I2) x R2 + (I1 – I3) x R3 – 14 V = 0
• Para la malla de la corriente I2:  -(I1 – I2) x R2 + 14 V + I2 x R4 – 12 V = 0
• Para la malla de la corriente I3:  -(I1 – I3) x R3 -12 V + I3 x R5 = 0

Con R1 = 10 ohmios, R2 = 6 ohmios, R3 = 4 ohmios, R4 = 8 ohmios, R5 = 2 ohmios

• Para la malla de la corriente I1:  10I1  + 6(I1 – I2) + 4(I1 – I3) – 14 V= 0
• Para la malla de la corriente I2:  -6(I1 – I2) + 14 V + 8I2 – 12 V = 0
• Para la malla de la corriente I3:  -4(I1 – I3) – 12 V + 2I3 = 0

Reacomodando las ecuaciones se obtienen:

Para la malla de la corriente I1:

(10 + 6 + 4)I1 – 6I2 – 4I3 – 14V = 0

20I1 – 6I2 – 4I3 = 14V

Para la malla de la corriente I2:

6I2 + 8I2 – 6I1 + 14V – 12V = 0

6I2 + 8I2 – 6I1  = -2V

Para la malla de la corriente I3:

4I3 + 2I3 – 4I1 = 12

Las ecuaciones finales son: (como se indica en el paso 4)

• 20I₁ – 6I₂ – 4I₃ = 14
• – 6I₁ + 14I₂ + 0I3  = -2
• – 4I₁  + 0I₂ + 6I₃ =  12

Como hay tres corrientes incógnitas, hay tres filas en la tabla. Utilizando el método de sustitución o con ayuda de determinantes se obtienen los siguientes valores:

• I₁ = 0.348 amperios
• I₂ = 0.006285 amperios
• I₃ = -1.768 amperios. El signo menos indica que el sentido de la corriente I₃ es opuesto al que se supuso al principio.

analisis-de-mallas-en-circuitos-resistivos