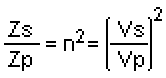- ¿Por qué acoplar impedancias para máxima transferencia de potencia?
- Adaptación de impedancias con transformador
- Cálculo de acople de impedancia con transformador
Antes de ver este tutorial se recomienda primero leer los tutoriales: Impedancia y Teorema Máxima transferencia de potencia.
¿Por qué adaptar impedancias para máxima transferencia de potencia?
En muchas ocasiones es necesario hacer una conexión entre dos equipos o un equipo y una carga con el propósito de pasar información de uno a otro. Hay dos opciones de acoplamiento:
- Para máxima transferencia de potencia o …
- Para una tensión máxima en la señal a transmitir.
Acoplar impedancia para máxima transferencia de potencia
Acoplar impedancia significa lograr que la impedancia de salida de la fuente y la impedancia de entrada de la carga sean “iguales”. Se tiene que acoplar la impedancia de salida de una fuente de señal con la impedancia de entrada de la carga, de manera que exista una máxima transferencia de potencia y se minimice las reflexiones causadas por la carga.
Nota: cuando hay reflexiones, parte de la potencia de la señal que se desea transmitir, se regresa a la fuente. Estas reflexiones, si son muy grandes, podrían dañar la fuente de señal.
En un acoplamiento para la transmisión de señales de un gran ancho de banda y para evitar las reflexiones de la carga, la carga debe ser totalmente resistiva, y se debe acoplar perfectamente a la impedancia de la fuente (también totalmente resistiva).
Si se utiliza una línea de transmisión entre la fuente y la carga, entonces: Zcarga = Zlínea = Zfuente
Donde:
- Z = impedancia
- Zlínea = impedancia característica de la línea de transmisión
Aunque, como ya se dijo antes, tanto la impedancia de la fuente como de la carga deben ser totalmente resistivas, siempre se mantiene el nombre de acople de impedancias para referirse a esta operación. La aparición de una reactancia, sea en la fuente o en la carga, causará que el acople no se logre.
Acople de impedancias reactivas
En el caso de que tanto la fuente como la carga sean reactivas, se puede hacer un acople de impedancia para una sola frecuencia (tomar en cuenta que la reactancia varía con la frecuencia).
Si la frecuencia de la señal se mantiene, también se logra minimizar las reflexiones y se logra máxima transferencia de potencia. Para adaptar impedancias, se utilizan combinaciones de inductores, condensadores y transformadores.
En el caso de los transformadores, estos tienen:
- En el bobinado con mayor número de vueltas, más impedancia y …
- En el bobinado con menor número de vueltas una impedancia menor
Acordarse de que en teoría la potencia de entrada a un transformador se transfiere a la salida (menos algunas pérdidas).
Adaptación de impedancias con transformador
Cuando se desea hacer una adaptación de impedancias con transformador, lo que se pretende es que la impedancia de salida de la fuente sea la misma que la impedancia de entrada de la carga. Con esto se logra una maximizar la transferencia de potencia entre ambas partes.
La siguiente fórmula nos permite hacer los cálculos que nos ayudarán a lograr nuestro objetivo.
Donde:
- Zp: impedancia reflejada al primario cuando en el secundario la carga es Zs.
- Zs: impedancia reflejada al secundario cuando la impedancia conectada en el primario es Zp.
- n: es la relación de vueltas entre el bobinado primario y el secundario. n = Vs/Vp = Ip/Is
Ejemplo: Se tiene una carga de 80 ohmios conectada en el secundario de un transformador. Si n = 3, ¿cuál es la impedancia que se ve desde el bobinado primario?
De la fórmula anterior Zp = Zs/n2 —> Zp = 80/32 = 80/9 = 8.89 ohmios
Con el ejemplo anterior se demuestra que, con el transformador adecuado, se puede reflejar una impedancia con un valor en el secundario a otro valor diferente en el primario.
Cálculo de acople de impedancia con transformador
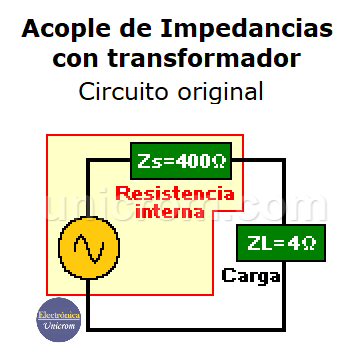
Supongamos que tenemos una fuente de voltaje (VAC) con una resistencia interna de 400 ohmios y esta debe alimentar una carga de 4 ohmios.
Si conectamos la carga directamente a la fuente no habrá una máxima transferencia de potencia debido a que la resistencia interna de la fuente (400 ohmios) es diferente a la resistencia de carga (4 ohmios).
Acople de Impedancias con transformador – Circuito original
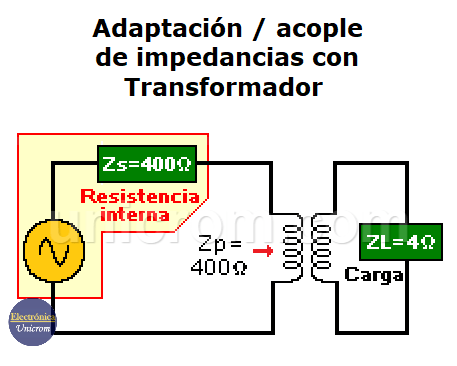
Para resolver el problema se incluye un transformador entre la fuente y la carga. Este debe de tener la relación de vueltas adecuada para lograr que la resistencia de 4 ohmios de la carga se refleje como si fuera de 400 ohmios a la fuente. Ver la siguiente imagen.
Adaptación / acople de impedancias con transformador
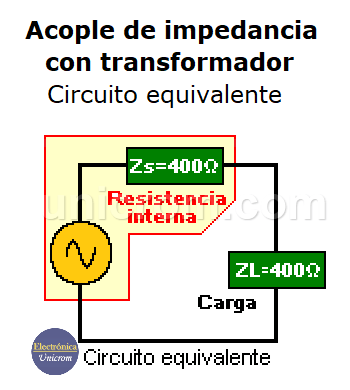
El circuito equivalente se muestra a continuación:
Acople de impedancia con transformador – Circuito equivalente
En este caso la resistencia interna y la resistencia reflejada del secundario al primario de transformador son iguales y hay máxima transferencia de potencia. n2 = Zs/Zp = 4/400 = 0.01, lo que significa que n = 0.1
Usando la siguiente fórmula: n = Vs/Vp —-> Vs = nVp y reemplazando se obtiene:
Vs = 0.1Vp ó lo que es lo mismo: Vp = 10 Vs.
Se puede deducir que se necesita un transformador con un número de espiras en el primario 10 veces mayor que en el secundario.
