Mapas de Karnaugh – Simplificación de funciones booleanas

¿Qué son los Mapas de Karnaugh?

Los Mapas de Karnaugh son una herramienta muy utilizada para la simplificación de circuitos lógicos. Cuando se tiene una función lógica con su tabla de verdad y se desea implementar esa función de la manera más simple y económica posible, se utiliza este método.

Ejemplos del uso de los Mapas de Karnaugh

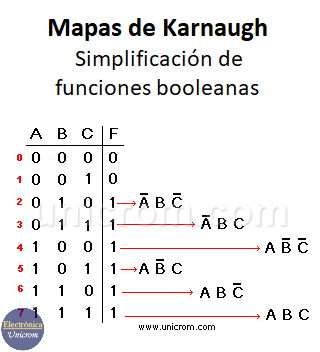
Ejemplo 1: Se tiene la siguiente tabla de verdad para tres variables. Se desarrolla la función lógica basada en ella. (primera forma canónica).

F = A B C + A B C + A B C + A B C + A B C + A B C

Ver que en la fórmula se incluyen solamente las variables (A, B, C) cuando F cuando es igual a “1”. Si A en la tabla de verdad es “0” se pone A, si B = “1” se pone B, Si C = “0” se pone C, etc.

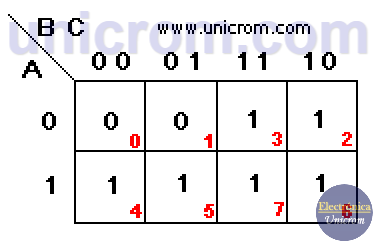
Una vez obtenida la función lógica, se implementa el mapa de Karnaugh. Este tiene 8 casillas que corresponden a 2ⁿ, donde n = 3 (número de variables (A, B, C)). Ver el diagrama siguiente.

• La primera fila corresponde a A = 0
• La segunda fila corresponde a A = 1

• La primera columna corresponde a BC = 00 (B = 0 y C = 0).
• La segunda columna corresponde a BC = 01 (B = 0 y C = 1).
• La tercera columna corresponde a BC = 11 (B = 1 y C = 1)
• La cuarta columna corresponde a BC = 10 (B = 1 y C = 0)

En el mapa de Karnaugh se han puesto “1” en las casillas que corresponden a los valores de F = “1” en la tabla de verdad. Tomar en cuenta la numeración de las filas de la tabla de verdad y la numeración de las casillas en el mapa de Karnaugh.

Para proceder con la simplificación, se crean grupos de “1”s que tengan 1, 2, 4, 8, 16, etc. (solo potencias de 2). Los “1”s deben estar adyacentes (no en diagonal) y mientras más “1”s tenga el grupo, mejor.

La función mejor simplificada es aquella que tiene el menor número de grupos con el mayor número de “1” s en cada grupo

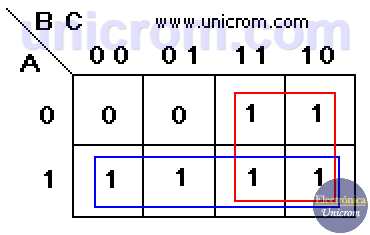
Se ve del gráfico que hay dos grupos cada uno de cuatro “1”s (se permite compartir casillas entre los grupos). La nueva expresión de la función booleana simplificada se deduce del mapa de Karnaugh.

• Para el primer grupo (rojo): la simplificación da B (los “1”s de la tercera y cuarta columna corresponden a B sin negar)
• Para el segundo grupo (azul): la simplificación da A (los “1”s están en la fila inferior que corresponde a A sin negar).

Entonces el resultado es F = B + A  o   F = A + B

Ejemplo 2: Una tabla de verdad como la siguiente con su función booleana: F = A B C + A B C + A B C + A B C

Se ve claramente que la función es un reflejo del contenido de la tabla de verdad cuando F = “1”, Con esta ecuación se crea el mapa de Karnaugh y se escogen los grupos.

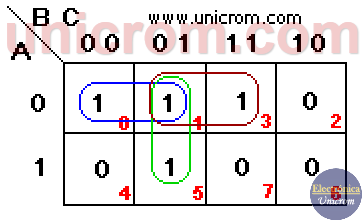
Se lograron hacer 3 grupos de dos “1”s cada uno. Se puede ver que no es posible hacer grupos de 3, porque 3 no es potencia de 2. Se observa que hay una casilla que es compartida por los tres grupos.

• El grupo en azul: A B
• El grupo marrón: A C
• El grupo verde: B C

La función simplificada es: F = A B+ A C + B C