Osciladores de cristal – Circuito equivalente, Impedancia

Osciladores de cristal

Por: Jonathan López, Chile. thanjonalopez@hotmail.com

Las sales de Rochelle, cuarzo, tumalina

Introducción: Las sales de Rochelle tienen la mayor actividad piezoeléctrica. Con una tensión alterna dada, vibran más que el cuarzo o la turmalina. Mecánicamente, son las más débiles porque se quiebran muy fácilmente. Estas sales se han empleado para hacer micrófonos, agujas fonocaptoras, audífonos y altavoces.

La turmalina muestra actividad piezoeléctrica mínima, pero es la más resistente de las tres. Es también la más cara. Ocasionalmente, se usa en frecuencias muy altas.

El cuarzo ocupa un lugar intermedio entre la actividad piezoeléctrica de las sales de Rochelle y la dureza de la turmalina. Debido a su coste y su disponibilidad en la naturaleza, se utiliza ampliamente para hacer osciladores de RF y filtros.

El cristal de cuarzo es utilizado como componente de control de la frecuencia de circuitos osciladores, convirtiendo las vibraciones mecánicas en voltajes eléctricos a una frecuencia específica. Esto ocurre debido al efecto “piezoeléctrico”.

La piezo-electricidad es electricidad en las caras opuestas creada por una presión mecánica. De una manera similar, una tensión aplicada en las caras del cristal origina una distorsión mecánica en su superficie.

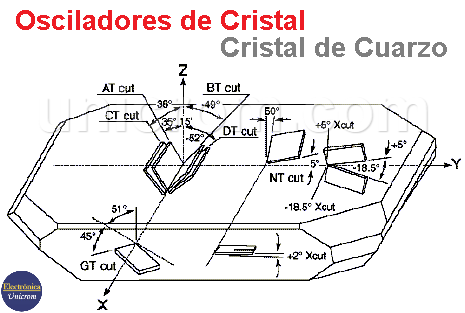
Una tensión alterna produce vibraciones mecánicas cuya frecuencia natural es muy estable, su amplitud tomará valores extremos para ciertas frecuencias. La frecuencia depende de la naturaleza y tallado del cristal, La siguiente figura muestra la ubicación de elementos específicos dentro de una piedra de cuarzo.

De los cortes que se pueden hacer, el corte “AT” es el más popular y es fabricado hasta frecuencias relativamente altas, mostrando una excelente estabilidad de frecuencia frente a las variaciones de la temperatura.

Por las propiedades mecánicas, eléctricas, y químicas, el cuarzo es el material más apropiado para fabricar dispositivos con frecuencia bien controlada. Por ejemplo, en dispositivos que funcionan a altas velocidades, en donde una pequeña variación en la frecuencia pudiera provocar un desfasamiento de la información a procesar.

El cristal de cuarzo ha sido utilizado por el humano por más de 100.000 años. El cuarzo está reconocido por su habilidad para producir impulsos eléctricos. Esta electricidad o impulso eléctrico que el cuarzo genera es un recurso muy importante en la tecnología actual.

Sonar, computadoras, relojes, aparatos eléctricos, radios y más, utilizan este increíble recurso de energía del cuarzo, que selecciona y separa una determinada vibración para que pueda ser usada sin la interferencia de otras.

El cristal de cuarzo:

• Amplifica: El sonido en micrófonos, bocinas y otras formas de audio y video.
• Transmite: Todo el espectro de la luz en lentes ópticos y prismas.
• Diagnóstica: Médicamente en microscopios y equipo de ultrasonido.
• Enfoca: La energía en la tecnología del rayo láser utilizado para medir la distancia de los planetas, quemar a través de un muro de acero, para efectuar microcirugías delicadas.
• Comunica: Las ondas de frecuencia en todos los rayos y estaciones transmisoras de T.V.
• Sincroniza: Con precisión el impulso del tiempo en los relojes a través de sus patrones vibratorios.

Circuito equivalente e impedancia resonante en osciladores a cristal

Marco teórico: Un oscilador a cristal es básicamente un oscilador de circuito sintonizado que usa un oscilador de cristal piezoeléctrico como circuito tanque resonante.

La analogía con los circuitos RLC se hace inevitable (aunque frente a esta comparación, el cristal piezoeléctrico presenta mayor estabilidad de frecuencia, es decir, un pico de resonancia más estrecho que el que podríamos obtener empleando componentes electrónicos comunes).

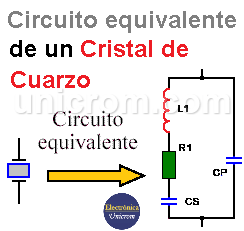
Si bien el modelo del circuito RLC Serie surge a priori como el indicado para describir el fenómeno, algunas consideraciones acerca del montaje experimental dan lugar a otro modelo algo similar, el de un circuito RLC montado en Paralelo con un capacitor. Tal como se muestra a continuación:

Cuando el cristal no está vibrando, es equivalente a una capacidad Cp por estar compuesto de dos placas de metal separadas por un dieléctrico. Cp, recibe el nombre de capacidad del encapsulado.

La inductancia L1 y la capacitancia Cs representan los equivalentes eléctricos de la masa y el comportamiento del cristal, mientras que la resistencia R es un equivalente eléctrico de la fricción interna de la estructura del cristal. La capacitancia en paralelo Cp representa la capacitancia debida al montaje mecánico del cristal.

Debido a que las perdidas del cristal, representadas por R1, son pequeñas, el Q (factor de calidad) equivalente del cristal es alto, por lo general de 20.000. Se pueden lograr valores de Q de casi 106 usando cristales.

El circuito eléctrico equivalente mostrado anteriormente, puede tener dos frecuencias resonantes. Una condición resonante sucede cuando las reactancias de la rama serie RLC son iguales (y opuestas). Para esta condición, la impedancia resonante en serie es muy baja (igual a R).

La otra condición resonante sucede a una frecuencia más alta, cuando la reactancia de la rama resonante serie es igual a la reactancia del condensador Cp. Esta es una resonancia paralela o condición antirresonante del cristal.

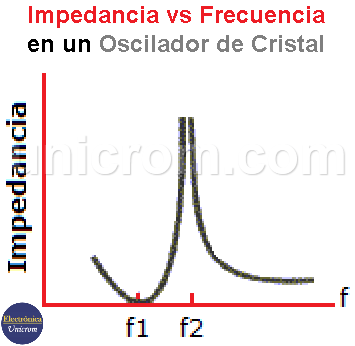
A dicha frecuencia, el cristal proporciona una impedancia muy alta al circuito externo. En la siguiente figura se muestra la impedancia del cristal en función de la frecuencia del cristal.

Para usar adecuadamente el cristal, debe estar conectado en un circuito que seleccione la baja impedancia en el modo de operación resonante en serie o alta impedancia en el modo de operación antirresonante.